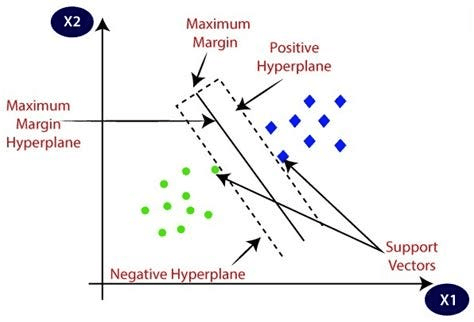
Support Vector

Study /

AI /

Machine Learning /

SVM /

Support Vector

Create : 2024년 12월 2일 18:20Update : 2025년 8월 22일 23:31

# Tag:

Source/KU_ML2

Support Vector

decision boundary 주변에서, 특정한 조건을 만족하는 일부 instance를 말한다.

이 instance와 decision boundary 사이의 거리를 margin이라고 하며, 이를 최대화 하는 것을 SVM이라고 한다.

Decision Boundary: HyperPlane(초평면). n차원에 그려진 초평면(n-1 차원)이, desicion boundary가 된다.
- $a x_{1} + b x_{2} + c x_{3} + d = 0$ : HyperPlane of 3 dim.
- Hyperplane : a surface generated by a straight line moving at a constant velocity. 2차원이라면, 3차원으로 그어진 HyperPlane이라 할 수 있다.

Optimal Seperating hyperplane

기본적으로, 간단하게 문제를 해결하기 위해 Linear Discriminant를 이용한다는 것을 전제로 한다. 이 때, driciminant function

g (x) = w^{⊤} x + w_{0}

이 0보다 큰 지, 작은 지에 따라 class를 이진 분류한다.

decision boundary 위의 점 $x_{1}$ 에 대해서, $w^{⊤} x_{1} + w_{0} = 0$ 이 된다.
$w$ 의 크기 $∥ w ∥$ 로 나누어, $w$ 를 단위 벡터로 취급하여 생각할 때, $\frac{w ^{t} x _{1}}{∥ w ∥} = - \frac{w _{0}}{∥ w ∥}$ 이다.

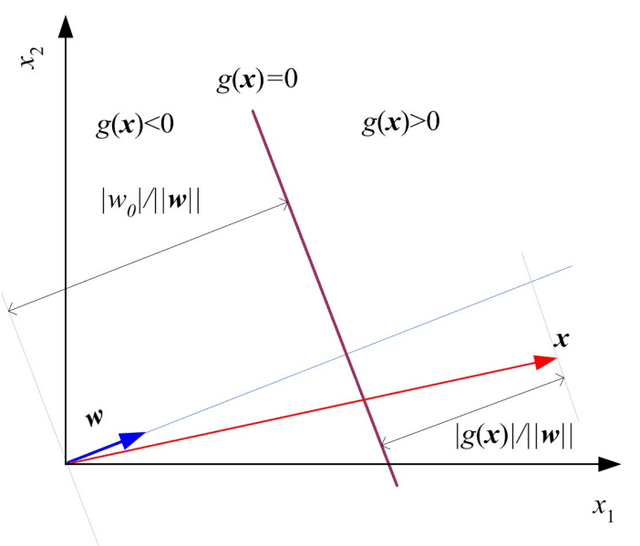
그렇다면, $x$ 에 대하여, 해당 instance를 어떤 class인지 분류하는 것은 decision boundary에서 얼마나 떨어져 있는지, distance를 측정하는 것으로 바꿀 수 있다.

distance \equiv \frac{w ^{t} x + w _{0}}{∥ w ∥}

이 0보다 큰 지, 작은 지에 따라 class가 분류된다.

$\frac{w _{0}}{∥ w ∥}$ 이 원점에서 decision boundary까지의 거리가 되므로 decision boundary의 우측에 있으면 거리가 0보다 클 것이고, 좌측에 있으면 거리가 0보다 작게 될 것이다.

$\frac{w _{0}}{∥ w ∥}$ 을 뺀다는 것은, 단위 벡터 $\frac{w}{∥ w ∥}$ 에 $x$ 를 곱한 것에, $x_{1}$ 이 decision boundary 위에 있으므로 decision boundary 까지의 거리를 잰다는 것과 동일해진다.
이러한 idea를 바탕으로 distance를 기반으로 분류하는 문제로 전환할 수 있다.

Margin으로의 전환

margin의 정확한 정의는, decision boundary에서 가장 가까운 instance까지의 distance이다.

이 때, optimal hyperplane은 margin이 가장 최대화 되는 hyperplane이다.

train data의 instance에 noise가 약간 낀 형태로 test data가 주어질 것이라는 믿음이 일반적이다. 따라서, train data에 noise가 껴서 decision boundary에 가까워져도 margin이 커야 잘 분류 가능할 것이다.
Nonparametric Methods처럼, 비슷한 값끼리는 모여 있을 것이니 최대한 margin을 크게 해야 비슷한 값끼리 잘 모여있는 것을 예측할 수 있을 것이다.
비슷한 input은, 보통 비슷한 output끼리 모여 있다.

label $r^{t}$ 를 편의를 위해 $r^{t} = {+ 1 - 1 if x^{t} is a positive if x^{t} is a negative$ 라고 하자.

위에서 정의된 $distance$ 에 따르면, $distance$ 가 0보다 작을 때는 negative, 0보다 클때는 positive이다. 이를 margin의 정의에 따르게 하려면

\frac{r ^{t} ( w ^{⊤} x ^{t} + w _{0} )}{∥ w ∥} \geq ρ, for all t

가 되도록 해야 한다. 즉, decision boundary까지의 거리가 모든 instance에 대해 margin $ρ$ 보다 커야 한다.

Maxinum Margin HyperPlane

r^{t} (w^{⊤} x^{t} + w_{0}) \geq ρ ∥ w ∥, for all t, ρ ∥ w ∥ \equiv 1

로 바꾸어 문제를 전환하자.
$ρ ∥ w ∥ \equiv 1$ 로 고정되게 정의하자면, $ρ$ 가 가장 커지게 하는 $w$ 를 찾는 문제가 된다. 실제로 $w$ 의 크기가 중요한 것이 아니라 그 방향이 중요하므로 해당 방식이 성립한다. 상수를 곱해도 optimization은 성립하기 때문이다.

w, w_{0} min \frac{1}{2} ∥ w ∥^{2}

: when $r^{t} (w^{⊤} x^{t} + w_{0}) \geq 1$ 이라는 constaints가 있는 optimization problem(Quadratic Programming)이 된다.

즉, $w$ 가 작아지면 $ρ$ 가 커지고, 적절한 방향으로 고정되는 constaints를 가진 optimization이 된다.

As Primal Problem

$L_{p} \equiv \frac{1}{2} ∥ w ∥^{2} - t \sum α^{t} (r^{t} (w^{⊤} x^{t} + w) - 1)$

: $α$ 는 Lagrange Multiplier이다.

이에 대해

w, w_{0} min α max L_{p}, α \geq 0 for all t

이다. $α \geq 0$ 은 constaints를 위한 조건이다.

constaints: $r^{t} (w^{⊤} x^{t} + w) - 1$ 에 대하여,

constrains < 0 : $α$ 가 무한에 가까워 질 수록 $max$ 가 성립한다. 이는, 해당 instance가 제약 조건이 성립하지 않으므로, margin 안에 존재하여 margin에 직접적인 영향을 미치는 경우이다. 즉, margin을 결정하는데 영향을 주도록 $α$ 가 커지도록 한다.
constrains $\geq$ 0: $α = 0$ 일 때, $max$ 가 성립한다. 이는, 해당 instance가 제약 조건이 성립해 margin 밖에 존재함을 의미한다. $α = 0$ 이 되도록 해, decision boundary 결정에 배제되도록 한다.

\frac{\partial L _{p}}{\partial w} = w - t \sum α^{t} r^{t} x^{t} = 0

\frac{\partial L _{p}}{\partial w _{0}} = t \sum α^{t} r^{t} = 0

As Dual Problem

하지만,

w

의 차원에 dependent하다.

$w$ 는 데이터의 feature 수와 같으므로 차원이 높을 경우 계산량이 급격히 증가한다. 따라서 Dual Problem으로 전환해 SVM에서 kernel trick을 위한 계산을 효율적이게 한다.

내적만 계산하면 되고, 보통 데이터의 샘플 수는 차원보다 작은 경우가 많아 compuation cost가 상당히 감소하게 된다.

Primal Problem의 Lagrangier function에, optimal 문제를 풀어 나온 결과를 대입하면

L_{d} \equiv \frac{1}{2} w^{⊤} w - w^{⊤} t \sum α^{t} r^{t} x^{t} - w_{0} t \sum α^{t} r^{t} + t \sum α^{t}

= - \frac{1}{2} (t \sum α^{t} r^{t} x^{t})^{⊤} t \sum α^{t} r^{t} x^{t} + t \sum α^{t}

= - \frac{1}{2} t \sum s \sum α^{t} α^{s} r^{t} r^{s} (x^{t})^{⊤} x^{s} + t \sum α^{t}

내적에 대한, $x$ 의 개수에 dependent한 문제로 바뀐다.

이 때, KKT Condition이 된다.

$α^{t} \geq 0$
$r^{t} (w^{⊤} x^{t} + w_{0}) - 1 \geq 0$
$α^{t} (r^{t} (w^{⊤} x^{t} + w_{0}) - 1) = 0$ : 둘 중 하나는 0

마찬가지로, Quadratic Programming 혹은 Gradient Descent(여기서는 gradient ascent, maximizing 해야 하므로)로 조건을 풀 수 있다.

Support Vector

따라서,

α^{t} > 0

을 만족하는, decision boundary 주변에 있는 몇개의 instance들을 support vector라고 한다.

모든 instance를 이용하지 않고 Support vector만을 이용해 optimal한 hyperplane을 결정할 수 있는 것이다.

Support Vector Subset을 $S$ 라 하고, 위의 조건대로 풀면

$α = 0$ : $r^{t} (w^{⊤} x^{t} + w_{0}) > 1, for x^{t} \in / S$
$α > 0$ : $r^{t} (w^{⊤} x^{t} + w_{0}) = 1, for x^{t} \in S$

w = t, α^{t} \neq = 0 \sum α^{t} r^{t} x^{t}

그리고, $∣ r^{t} ∣ = 1$ 이므로 $w^{⊤} x^{t} + w_{0} = r^{t} for any x^{t} \in S$ 이고,

w_{0} = r^{t} - w^{t} x^{t} for x^{t} \in S

과 같이 optimal decision boundary를 결정 할 수 있다.